This app calculates optimal solution to a problem involving a network. It may increase profits from your business. Contact us for further details.
The problem: Suppose there is a network of nodes. Each node is linked with a certain number of customers. Nodes are located in a square 25 km x 25 km, which reflects a city. The goal is to visit customers and deliver them physical products. The objective function is a profit.
Assumptions: area 25 km x 25 km, number of nodes 10, average car speed 50 km/h, fuel cost $0.5/km, driver cost $10/h, revenue $2/customer, time needed to serve all customers in a node 0.2 h/mode
Nodes:
| ID | X Coordinate | Y Coordinate | Number of Customers |
|---|---|---|---|
| 0 | 1 | 1 | 4 |
| 1 | 3 | 13 | 18 |
| 2 | 25 | 15 | 2 |
| 3 | 17 | 0 | 29 |
| 4 | 19 | 12 | 15 |
| 5 | 25 | 25 | 1 |
| 6 | 24 | 6 | 24 |
| 7 | 12 | 13 | 9 |
| 8 | 8 | 22 | 5 |
| 9 | 10 | 25 | 17 |
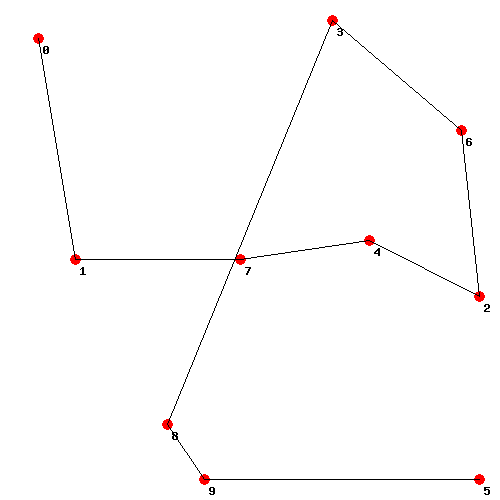
Optimal network graph. Case basic: 10 nodes, profit $161.08
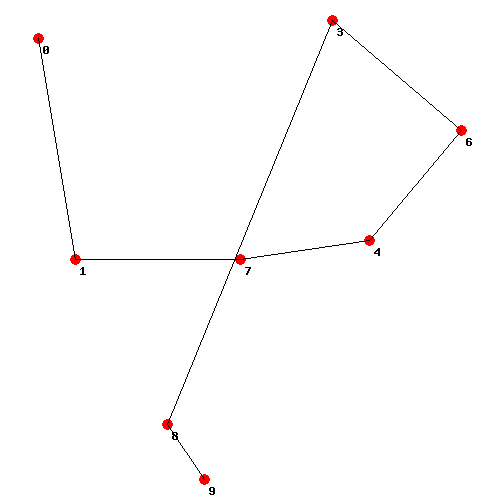
Optimal network graph. Case reduced: 8 nodes (excluding nodes 2 and 5), profit $171.15, i.e. + 6.25% vs case basic